9647. Optimal matrix multiplication

Given two matrices A and B, we can determine the matrix C = AB using the standard definition of matrix multiplication:

The number of columns in the matrix A must be the same as the number of rows in the matrix B. Let matrix A has size m × n, matrix B has size n × p. Then matrix С wil have the size m × p, and to calculate it you should perform m * n * p multiplications.

For example, if size of A is 10 × 20, size of B is 20 × 15, it will take 10 × 20 × 15 = 3000 multiplications to compute matrix C.

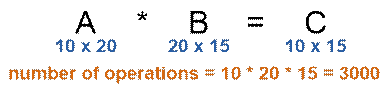
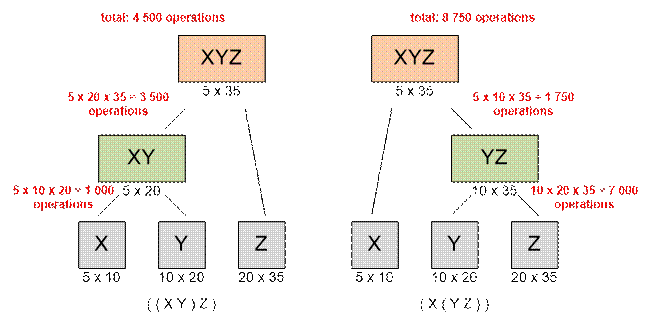
Multiplication of more than two matrices can be done in multiple ways. For example, if X, Y and Z are matrices, then XYZ computation can be done either like (XY)Z or X(YZ). Let size of X be 5 × 10, size of Y be 10 × 20, and size of Z be 20 × 35.

Let’s look at the number of multiplications required to compute the product using two different ways:

(XY)Z

· 5 × 10 × 20 = 1000 multiplications to determine the product (XY) that has size 5 × 20.

· Then 5 × 20 × 35 = 3500 multiplications to find the final result.

· Total number of multiplications: 4500.

X(YZ)

· 10 × 20 × 35 = 7000 multiplications to determine the product (YZ) that has size 10 × 35.

· Then 5 × 10 × 35 = 1750 multiplications to find the final result.

· Total number of multiplications: 8750.

Clearly we'll be able to compute (XY)Z using fewer multiplications.

Given the sequence of matrices to be multiplied, you are to determine the optimal order of their multiplication. Optimality in this problem is relative to the number of scalar multiplications required.

Input. First line contains the number n (n ≤ 10) of matrices to be multiplied. It is followed by n pairs of integers, each pair giving the number of rows and columns in a matrix, matrix sizes are given in the order of their multiplication.

Output. Print the minimum number of multiplications sufficient to multiply all matrices.

Sample input 1	Sample output1
3 5 10 10 20 20 35	4500
Sample input 2	Sample output 2
6 30 35 35 15 15 5 5 10 10 20 20 25	15125

SOLUTION

dynamic programming

Algorithm analysis

Let A_ij denote the product of matrices A_i * A_i+1 * … * A_j-1 * A_j (1 £ i £ j £ n). Let m[i, j] represent the minimum number of multiplications required to compute A_ij. The cost of computing the entire product A_1n will be stored in m[1, n]. The values m[i, i] = 0 since A_ii = A_i, and no computations are required for its evaluation.

The number of columns in matrix A_i equals the number of rows in matrix A_i+1. This value is stored in p[i]. The number of rows in matrix А₁ is stored in p[0], and the number of columns in matrix A_n is stored in p[n].

Suppose that in the optimal parenthesization of the product A_i * … * A_j, the final multiplication is

(A_i * … * A_k ) * (A_k+1 * … * A_j)

The value of m[i, j] is equal to the sum of the minimum computation costs of A_ik and A_k+1j, plus the cost of multiplying these two matrices:

m[i, j] = m[i, k] + m[k + 1, j] + p[i – 1] * p[k] * p[j]

Here, the value of k can take only j – i different values: i, i + 1, …, j – 1. Since only one of these is optimal, it is necessary to iterate through all these values and select the best one. As a result, we derive the recurrence relation:

m[i, j] =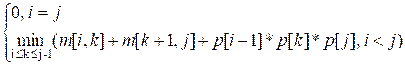

To store the optimal order of multiplication, we define s[i, j] = k, if in the optimal computation of A_i * … * A_j, the final operation is multiplying A_i * … * A_k by A_k+1 * … * A_j.

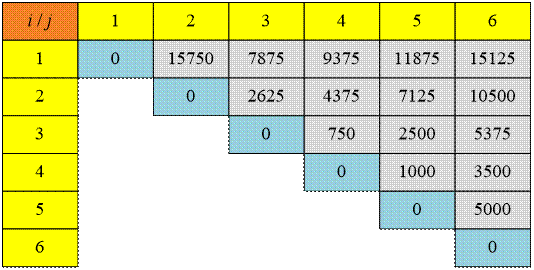
Example

Let’s consider the second test case. The data on the dimensions of the input matrices is stored in the array p:

The minimum cost of computing the matrices A_ij is stored in the cells of the array m[i, j]:

The corresponding values of the matrix s:

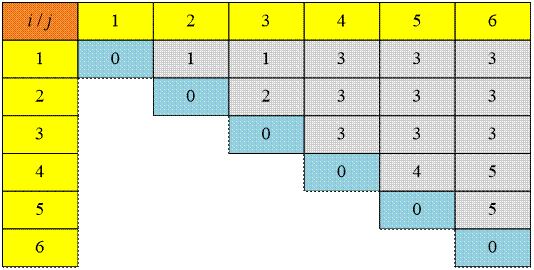
To multiply six input matrices, it is sufficient to perform m[1,6] = 15125 multiplication operations. The optimal multiplication sequence is as follows:

A₁₆ = (s[1,6] = 3) = A₁₃ * A₄₆ =

(s[1,3] = 1, s[4,6] = 5) = (A₁₁ * A₂₃) * (A₄₅ * A₆₆) =

(s[2,3] = 2, s[4,5] = 4) = (A₁₁ * (A₂₂ * A₃₃ ) ) * ((A₄₄ * A₅₅) * A₆₆) =

(A₁ * (A₂ * A₃ ) ) * ((A₄ * A₅) * A₆)

Algorithm realization

Declare the constants INF = ∞, MAX = 11 (maximum possible number of matrices in the product). Declare arrays dp and p.

#define INF 0x3F3F3F3F3F3F3F3F

#define MAX 11

long long dp[MAX][MAX], p[MAX];

The Mult function returns the minimum number of multiplications sufficient to compute A_ij = A_i * A_i+1 * … * A_j-1 * A_j, which is saved in the cell dp[i][ j].

long long Mult(int i, int j)

{

if (dp[i][j] == INF)

for (int k = i; k < j; k++)

dp[i][j] = min(dp[i][j], Mult(i, k) + Mult(k + 1, j) +

p[i - 1] * p[k] * p[j]);

return dp[i][j];

}

The main part of the program. Read the number of matrices n.

scanf("%d",&n);

Set all cells in dp array to infinity (∞).

memset(dp,0x3F,sizeof(dp));

Read the sizes of the input matrices, store them in the array p. Assign dp[i][i] = 0.

for(i = 1; i <= n; i++)

{

scanf("%lld %lld",&p[i-1],&p[i]);

dp[i][i] = 0;

}

Compute the result, we are looking for the optimal product of matrices A₁ * A₂ * … * A_n-1 * A_n.

Mult(1,n);

Print the answer that is located in the cell dp[1][n].

printf("%lld", dp[1][n]);